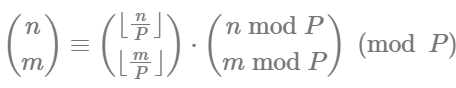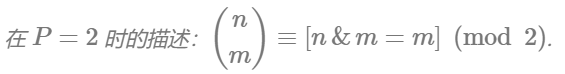【2024-ZR-C Day 1】数论基础
作者:Heartquakes,发表于 Wed Jul 17 2024。
1. Ex-GCD
1.1. 定义
若 $(a, b)=1$,则必然存在整数 $x$ 使得 $ax \equiv 1 (\bmod b)$.
即:$ax+by=\gcd(a, b)$,$x, y$ 必然有解。
1.2. 裴蜀定理
推论:若 $(a, b)=1$,则必然存在整数 $x, y$ 满足 $ax + by = 1$.
裴蜀定理:对于 $a, b \in \mathbb{Z}$,$\exists x, y: ax + by = (a, b)$.
证明:记 $d = (a, b), \space a' = \frac{a}{d}, \space b' = \frac{b}{d}$, 由 Ex-GCD 的推论知存在 $x, y$ 满足 $a'x+b'y = 1$. 左右同乘 $d$,得 $ax + by = d$.
1.3. 求解
如何求出 $x, y$?
定义 $f(a, b)$:给定 $a, b$,求出任意一组合法的 $x, y$.
有基本事实:$a \bmod b = a - \lfloor \frac{a}{b} \rfloor \times b$. 那么考虑通过 $f(b, a \bmod b)$ 推出 $f(a, b)$.
记 $t = \lfloor \frac{a}{b} \rfloor$,则 $a \bmod b = a-tb$. $f(b, a \bmod b)$ 满足方程 $bx + (a \bmod b) y = d$,即 $bx + (a - tb) y = d$. 而 $f(a, b)$ 需要满足的方程为 $ax' + by' = d$,令 $x' = y, \space y' = x - ty$ 即可。
void exgcd(int a, int b, int &x, int &y)
{
if(!b) {x = 1, y = 0; return a;}
exgcd(b, a % b, y, x);
int xx = x, yy = y, t = a / b;
x = yy, y = xx - t * yy;
return;
}
可以证明,即使 $a, b \le 10^9$,也绝对不会爆 int.
2. 扩展中国剩余定理(Ex-CRT)
形如以下样式的同余方程组:
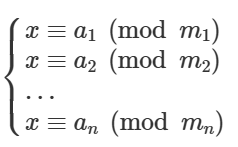
考虑合并以下方程组:
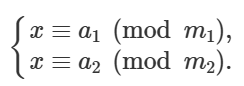
此方程组等价于 $x = m_1 \cdot u + a_1 = m_2 \cdot v + a_2$.
移项,得 $m_1 \cdot u - m_2 \cdot v = a_2 - a_1$.
记 $d = \gcd(m_1, m_2), \space p_1 = \frac{m_1}{d}, \space p_2 = \frac{m_2}{d}$, 则上式可写作 $p_1 \cdot u - p_2 \cdot v = \frac{a_2 - a_1}{d}$(*).
可先用 Ex-GCD 求出方程 $\lambda_1p_1 + \lambda_2p_2 = 1$. 则可以拼出 $u, v$ 的值:
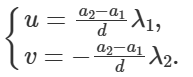
(将 $u, v$ 带入(*)式,发现确实为一组解。)
于是有一个解 $x' = m_1 \cdot u + a_1 = a_1 + \frac{a_2 - a_1}{d} \lambda_1 \cdot m_1$.
可以合并出一个新的方程组 $x \equiv x' = a_1 + \frac{a_2 - a_1}{d} \lambda_1 \cdot m_1 \space \pmod{\operatorname{lcm}(m_1, m_2)}$.
从 $1$ 开始,每次合并两个方程,最终剩下一个的 $a$ 值即为答案。
3. 乘法逆元
3.1. 定义
定义:若 $ax \equiv 1 \pmod{P}$,则称 $x$ 为 $a$ 模 $P$ 的乘法逆元.
3.2. Wilson 定理
Wilson 定理:给定质数 $P$,$(P-1)! \equiv -1 \pmod{P}$.
考虑将 $[1, P-1]$ 中的数及逆元两两配对,能配对当且仅当 $a \ne a^{-1} \pmod{P}$. 即不能配对当且仅当 $x^2 = 1 \pmod{P}$,只有一个解 $x = P-1$. 故 $(P-1)! \equiv P - 1 \equiv -1 \pmod{P}$.
3.3. 费马小定理
费马小定理:对于质数 $P$ 和非 $0$ 整数 $a$,$a^{P-1} \equiv 1 \pmod{P}$.
证明:注意到 $a, 2a, \ldots, (n-1)a$ 在 $\bmod P$ 意义下取遍 $[1, P - 1]$ 中所有数, 考虑 $1 \cdot 2 \cdot 3 \cdots (P - 1) \equiv (1a) \cdot (2a) \cdot (3a) \cdots [(P-1) a]$, 即 $(P - 1)! \equiv a^{P - 1}(P - 1)!$. 由 Wilson 定理得,$-1 \equiv -1 \cdot a^{P - 1}$. 即 $a^{P-1} \equiv 1 \pmod{P}$.
由此,$a^{P - 2} \equiv -1 \pmod{P}$,即为 $a$ 模 $P$ 的乘法逆元。
3.4. 欧拉定理
欧拉定理:对于 $(a, m) = 1$,有 $\varphi(m) \equiv 1 \pmod{m}$. 其中,$\varphi(m)$ 表示 $[1, m]$ 里和 $m$ 互质的数的个数。
3.5. 预处理逆元
引入:给定质数 $P$,多次询问 $\begin{pmatrix}n \ m \end{pmatrix} \bmod P$.
$i! = (i - 1)! \cdot i$,则 $\frac{1}{(i - 1)!} = \frac{1}{i!} \cdot i$.
注意到 $\frac{1}{(i - 1)!}$ 和 $\frac{1}{i!}$ 在 $\bmod P$ 意义下分别为 $(i - 1)!$ 和 $i!$ 的逆元,就可以线性预处理阶乘的逆元了。
注意到 $i = i! \cdot [(i-1)!]^{-1}$,则 $i^{-1} = \frac{1}{i!} \cdot (i-1)!$. 即可以用阶乘的逆元和阶乘来 $O(1)$ 计算逆元。
int ifac[N], inv[N], fac[N];
void init(int n)
{
fac[0] = 1;
for(int i= 1; i <= n; i++)
fac[i] = 1ll * fac[i - 1] * i % P;
ifac[n] = ksm(fac[n], P - 2);
for(int i = n; i >= 1; i--)
{
ifac[i - 1] = 1ll * inv[i] * i % P;
inv[i] = 1ll * fac[i - 1] * ifac[i] % P;
}
return;
}
3.6. Lucas 定理
Lucas 定理:
,其中 $P$ 是质数.
使用 Lucas 求解的时间复杂度:$O(\log_P n)$
4. BSGS (Baby Step Gaint Step)
离散对数问题:给定 $a, b, P$,满足 $(a, P) = 1$,求出一个 $t$ 使得 $a^t \equiv b \pmod{P}$(也即求出模 $P$ 意义下的 $log_a b$)。
思考:给定 $P, a$ 和两个数的集合 $S, T$,找到一组 $x \in S, y \in T$ 使得 $xy \equiv a \pmod{P}$.
上式可以化为 $x \equiv \frac{a}{y}$. 考虑枚举 $x$ 的所有取值,将它们放入 Hash 表中;再枚举 $y$ 的所有取值,查询 Hash 表中是否有此值。时间复杂度 $O(\max{|S|, |T|} \log P)$.
回到原题,令 $B = \lceil \sqrt{P} \rceil$,取 $S = {a^i}, T = {a^{B\cdot i}}$ 即可,其中 $ \le i \le B$. 按照上面思考的方法即可解决问题,时间复杂度 $O(\sqrt{P} \log P)$.
#include <bits/stdc++.h>
using namespace std;
#define int long long
int p, b, n;
map<int, int> mp;
signed main()
{
ios :: sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> p >> b >> n;
int t = ceil(1.0 * sqrt(p)), g = 1;
for(int i = 0, r = n; i <= t; i++, r = r * b % p) mp[r] = i;
for(int i = 1; i <= t; i++) g = g * b % p;
for(int i = 1, r = g; i <= t; i++, r = r * g % p)
if(mp.count(r)) {cout << i * t - mp[r] << '\n'; return 0;}
cout << "no solution";
return 0;
}
5. Ex-BSGS
在 BSGS 中,要求了 $(a, P) = 1$,若这两数不互质,如何做?
考虑将 $a, P$ 转化为互质的。
设 $d = \gcd(a, P)$,则只需找到方程 $\frac{a}{d} \cdot a^{x-1} \equiv \frac{b}{d} \pmod{ \frac{P}{d}}$ 的解,即为原方程的解。
原方程即为 $a^{x-1} \equiv \frac{b}{d} \cdot (\frac{a}{d})^{-1} \pmod{\frac{P}{d}}$. 令 $b' = \frac{b}{d} \cdot (\frac{a}{d})^{-1}$,原方程化为 $a^{x-1} \equiv b' \pmod{\frac{P}{d}}$.
不断地进行 $(a, P) \to (a, \frac{P}{d})$,直到 $(a, P) = 1$,即变为普通的 BSGS 问题。
#include <bits/stdc++.h>
using namespace std;
#define int long long
void exgcd(int a, int b, int &x, int &y)
{
if(!b) {x = 1, y = 0; return;}
exgcd(b, a % b, x, y);
int xx = x, yy = y, t = a / b;
x = yy, y = xx - t * yy;
return;
}
inline int BSGS(int a, int b, int p)
{
map<int, int> mp;
int t = ceil(1.0 * sqrt(p)), g = 1;
for(int i = 0, r = b; i <= t; i++, r = r * a % p) mp[r] = i;
for(int i = 1; i <= t; i++) g = g * a % p;
for(int i = 1, r = g; i <= t; i++, r = r * g % p)
if(mp.count(r)) return i * t - mp[r];
return -1;
}
int exBSGS(int a, int b, int p)
{
if(b == 1 || p == 1) return 0;
int d = __gcd(a, p), x, y;
if(d == 1) return BSGS(a, b, p);
if(b % d) return -1;
p /= d;
exgcd(a / d, p, x, y);
int inv = (x + p) % p;
int res = exBSGS(a % p, 1ll * b / d * inv % p, p);
return (~res ? res + 1 : -1);
}
signed main()
{
ios :: sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int a, b, p;
while(cin >> a >> p >> b)
{
if(!a && !p && !b) return 0;
// cout<<a << p <<b;
int res = (b % p == 1 ? 0 : exBSGS(a % p, b % p, p));
if(~res) cout << res << "\n";
else cout << "No Solution" << "\n";
}
return 0;
}
6. 阶与原根
模 $m$ 的阶:最小的 $t$ 使得 $x^t \equiv 1 \pmod{m}$. 模 $m$ 的原根:模 $m$ 的阶为 $\varphi(m)$ 的数。
原根的本质:取对数将乘法转化成指数上的加法。
一个数 $m$ 存在原根当且仅当 $m = 2, 4, p^{\alpha}, 2p^{\alpha}$,其中 $p$ 为奇素数。、
如何快速判定一个数是否是原根?
引理:一个数模 $m$ 的阶如果存在,那它一定是 $\varphi(m)$ 的约数。
设 $m \ge 3, \space (g, m) = 1$,则 $g$ 是模 $m$ 的原根的充要条件是:对于 $\varphi(m)$ 的每个素因数 $p$,都有 $g^{\frac{\varphi(m)}{p}} \ne 1 \pmod{m}$.
推论:若一个数 $m$ 有原根,则它原根的个数为 $\varphi(\varphi(m))$.
7. 例题
7.1. P2480 [SDOI2010] 古代猪文
简要题意:求 $g^{\sum_{d | n} \begin{pmatrix}n \ d \end{pmatrix}} \mod P$,其中 $P = 999911659$,是一个质数。
根据欧拉定理的推论,$g^{\sum_{d | n} \begin{pmatrix}n \ d \end{pmatrix}} = g^{\sum_{d | n} \begin{pmatrix}n \ d \end{pmatrix} \mod (P - 1)}$.
可得 $P - 1 = 999911658 = 2\times 3\times 4679\times 35617$.
分别计算出 $\sum_{d | n} \begin{pmatrix}n \ d \end{pmatrix}$ 对以上四个数取模的结果,记为 $a_1, a_2, a_3, a_4$.
则有方程组
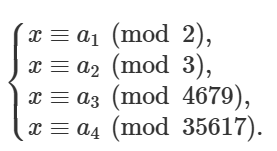
使用 CRT 解决即可。