动态DP Dynamic^2 Programming
作者:XiaoQuQu,发表于 Mon Jul 08 2024。
考虑定义一个矩阵乘法:$A\times B=C$ 为 $C_{i,j}=\max_{k=1}^ma_{i,k}+b_{k,j}$,我们称这里的 $\max$ 为外部运算,$+$ 为内部运算,一个新定义的矩阵乘法满足结合律当且仅当:
- 外部运算满足结合律,$\max(a,\max(b,c))=\max(\max(a,b),c)$;
- 内部运算满足结合律,$(a+b)+c=a+(b+c)$;
- 外部运算对内部运算有分配律,$\max(a+c,b+c)=\max(a,b)+c$,也就是说可以把内部运算中的外部运算提出来,比如 $a\times c+b\times c=(a+b)\times c$。
考虑:这个题。给定一棵树,点有点权,有修改,每次修改后求这棵树的最大权独立集的权值大小,$n,q\le 10^5$。
先考虑不带修改我们怎么做,设 $f_{i,0}$ 表示考虑 $i$ 子树且 $i$ 不选的最大权,$f_{i,1}$ 表示考虑 $i$ 子树选了 $i$ 的最大权。一个非常显然的转移是 $$ f_{i,0}=\sum\limits_{j \text{ is son of } i}\max(f_{j,0},f_{j,1}) $$
$$ f_{i,1}=\sum\limits_{j \text{ is son of }i}f_{j,0} + a_i $$
我们会发现每次修改节点 $x$ 的权值,只会影响到 $i$ 所在的这条链的所有 $f$,但是如果我们每次修改暴力重算 $x$ 这条链上的所有节点的 $f$ 是 $O(n)$ 的,于是考虑把树链剖分结合进来优化这个东西。
设 $g_{i,0},g_{i,1}$ 表示考虑 $i$ 子树,不选/选节点 $i$ 且不考虑重儿子的答案,设 $s$ 为 $i$ 的重儿子,于是我们有 $f_{i,0}=g_{i,0}+\max(f_{s,0},f_{s,1}),f_{i,1}=g_{i,1}+f_{s,0}$。考虑这个东西怎么结合我们上面定义的矩阵乘法。发现可以写成这样的转移:
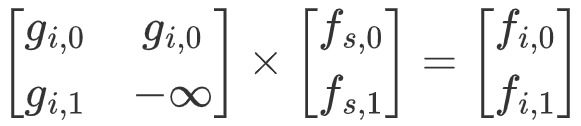
通过这样,每次更新节点 $x$ 的时候,我们只会修改从 $x$ 到根节点的每个轻重链交界处的 $g$,而无需修改重链内部的 $g$(因为 $g$ 代表我们不考虑重儿子),又因为从一个节点到根节点最多有 $O(\log n)$ 次轻重链切换,所以时间复杂度是可以保证的。
接下来考虑如何维护这个矩阵。我们树链剖分之后,可以使用个线段树来维护,每个线段树节点都维护一个矩阵,表示所在区间内的转移矩阵之乘积。在此题中,对于叶子节点,$g_{i,0}=f_{i,0},g_{i,1}=f_{i,1}$,所以我们只需要求出节点 $1$ 所在的重链的转移矩阵(重链的末尾一定是一个叶子节点),最终取一个 $\max$ 即可。
时间复杂度 $O(n\log^2n)$。
const int MAXN = 1e5 + 5;
int n, m, a[MAXN], tot, fa[MAXN], sz[MAXN], son[MAXN], dfn[MAXN], top[MAXN], ed[MAXN], f[MAXN][2], g[MAXN][2];
vector<int> G[MAXN];
struct _matrix {
int m[2][2];
_matrix() {
m[0][0] = m[0][1] = m[1][0] = m[1][1] = INT_MIN;
}
_matrix operator * (const _matrix &b) const {
_matrix ret;
for (int i = 0; i < 2; ++i) {
for (int j = 0; j < 2; ++j) {
for (int k = 0; k < 2; ++k) {
ret.m[i][j] = max(ret.m[i][j], m[i][k] + b.m[k][j]);
}
}
}
return ret;
}
} tr[MAXN << 2], val[MAXN];
struct _sgt {
void pushup(int p) {
tr[p] = tr[lson] * tr[rson];
}
void build(int p, int l, int r) {
if (l == r) return tr[p] = val[l], void();
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(p);
}
void update(int p, int l, int r, int x) {
if (l == r) return tr[p] = val[x], void();
if (x <= mid) update(lson, l, mid, x);
if (mid < x) update(rson, mid + 1, r, x);
pushup(p);
}
_matrix query(int p, int l, int r, int L, int R) {
if (L <= l && r <= R) return tr[p];
if (L <= mid && mid < R) return query(lson, l, mid, L, R) * query(rson, mid + 1, r, L, R);
if (L <= mid) return query(lson, l, mid, L, R);
if (mid < R) return query(rson, mid + 1, r, L, R);
}
} t;
void dfs1(int x, int fat) {
sz[x] = 1;
fa[x] = fat;
f[x][1] = a[x];
for (auto u:G[x]) {
if (u == fat) continue;
dfs1(u, x);
sz[x] += sz[u];
f[x][0] += max(f[u][0], f[u][1]);
f[x][1] += f[u][0];
if (sz[u] > sz[son[x]]) son[x] = u;
}
}
void dfs2(int x, int fat, int tp) {
dfn[x] = ++tot;
top[x] = tp;
ed[tp] = dfn[x];
if (son[x]) {
dfs2(son[x], x, tp);
}
g[x][1] = a[x];
for (auto u:G[x]) {
if (u == fat || u == son[x]) continue;
dfs2(u, x, u);
g[x][0] += max(f[u][1], f[u][0]);
g[x][1] += f[u][0];
}
val[dfn[x]].m[0][0] = g[x][0];
val[dfn[x]].m[0][1] = g[x][0];
val[dfn[x]].m[1][0] = g[x][1];
val[dfn[x]].m[1][1] = INT_MIN;
}
void modify(int x, int w) {
val[dfn[x]].m[1][0] += w - a[x];
a[x] = w;
while (x) {
auto last = t.query(1, 1, n, dfn[top[x]], ed[top[x]]);
t.update(1, 1, n, dfn[x]);
auto now = t.query(1, 1, n, dfn[top[x]], ed[top[x]]);
x = fa[top[x]];
val[dfn[x]].m[0][0] += max(now.m[0][0], now.m[1][0]) - max(last.m[0][0], last.m[1][0]);
val[dfn[x]].m[0][1] = val[dfn[x]].m[0][0];
val[dfn[x]].m[1][0] += now.m[0][0] - last.m[0][0];
}
}
void work() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> a[i];
for (int i = 1, u, v; i < n; ++i) {
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(1, 0);
dfs2(1, 0, 1);
t.build(1, 1, n);
for (int x, w, i = 1; i <= m; ++i) {
cin >> x >> w;
modify(x, w);
auto now = t.query(1, 1, n, dfn[1], ed[1]);
cout << max(now.m[0][0], now.m[1][0]) << endl;
}
}